21. Antiderivatives, Areas and the FTC
f. Fundamental Theorem of Calculus for Area
On the previous page we learned that the area function, \(A_a(x)\), is an antiderivative of the original function, \(f(x)\). This is actually the first version of the Fundamental Theorem of Calculus:
Given a positive function \(f(x)\) defined on an interval \([a,b]\), then its area function, \(A_a(x)\), is an antiderivative of the original function, \(f(x)\). In a formula: \[ \dfrac{d}{dx}A_a(x)=f(x) \]
The area function, \(A_a(x)\) is a specific antiderivative of \(f(x)\). So it differs from an arbitrary antiderivative \(F(x)\) by a constant. This constant is found by using the initial condition \(A_a(a)=0\). On the previous page, we did this for several specific functions \(f(x)\). Let's do this now for a general function \(f(x)\). In the process we will derive a general formula for \(A(a,b)\).
Find the area below a positive function \(y=f(x)\) above the \(x\)-axis between \(x=a\) and \(x=b.\)
Let \(A_a(x)\) be the area function for \(f(x)\) starting at \(x=a\). So \(A_a(x)\) is a specific antiderivative of \(f(x)\) which we write as: \[ A_a(x)=F(x)+C \] where \(F(x)\) is any antiderivative of \(f(x)\) and \(C\) is some constant. To find \(C\), we use the initial condition \(A_a(a)=0\) which says \[ A_a(a)=F(a)+C=0. \] Thus \(C=-F(a)\). Substituting back we find \(A_a(x)=F(x)-F(a)\). Then the area under \(f(x)\) above the interval \([a,b]\) is: \[ A(a,b)=A_a(b)=F(b)-F(a) \] This is the second version of the Fundamental Theorem of Calculus:
Given a positive function \(f(x)\) defined on an interval \([a,b]\), then the area under \(f(x)\) above the interval \([a,b]\) is: \[ A(a,b)=F(b)-F(a) \] where \(F(x)\) is any antiderivative of \(f(x)\).
We frequently write the right hand side of the last equation as \(\left.F(x)\rule{0pt}{10pt}\right|_a^b\) to mean that the function \(F(x)\) is evaluated at \(x=b\) and at \(x=a\) and then these values are subtracted. So we have: \[ A(a,b)=\left.F(x)\rule{0pt}{10pt}\right|_a^b=F(b)-F(a) \]
The following are the same example and exercise as on the previous page except solved by the Fundamental Theorem of Calculus.
Find the area below \(y=x^2\) above the \(x\)-axis between \(x=1\) and \(x=4\).
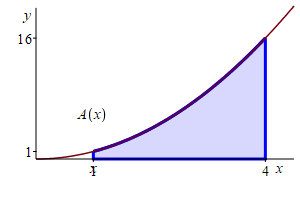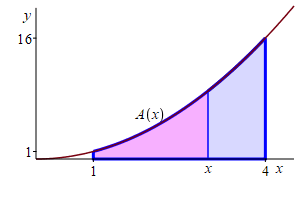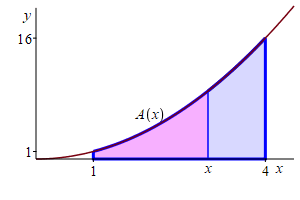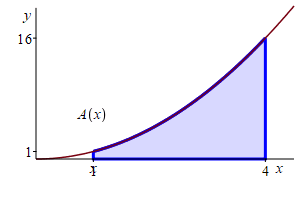
Let \(f(x)=x^2\). An antiderivative is \(F(x)=\dfrac{x^3}{3}\). So the area is \[ A(1,4)=\left.\dfrac{x^3}{3}\right|_1^4 =\dfrac{4^3}{3}-\dfrac{1^3}{3}=21 \]
Find the area below \(y=\sin(x)\) above the interval \([0,\pi]\).
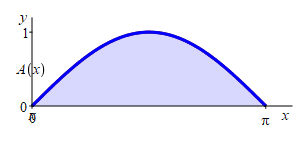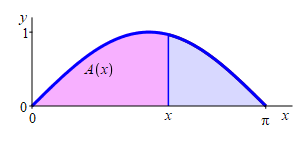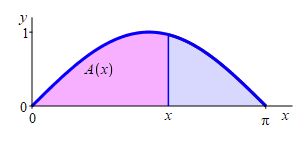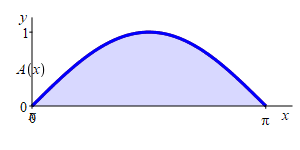
The area below \(y=\sin(x)\) above the interval \([0,\pi]\) is \(A(0,\pi)=2\).
An antiderivative of \(f(x)=\sin(x)\) is \(F(x)=-\cos(x)\). So the area is \[\begin{aligned} A(0,\pi)&=\left[\dfrac{}{}-\cos(x)\right]_0^\pi =-\cos(\pi)+\cos(0) \\ &=--1+1=2 \end{aligned}\]
Heading
Placeholder text: Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum